c) If n = 10 and p = 0.60, find P(x ≥ 7)
This is an at least problem, i.e. at least 7.
P(x ≥ 7) = 1 – P(x = 0) - P(x = 1) - P(x = 2) - P(x = 3) - P(x = 4) - P(x = 5) - P(x = 6)
|
P(x=r) |
|
nCx |
px |
qn-x |
|
|
|
P(x=0) |
= |
1 |
1.00000 |
0.00010 |
= |
0.0001 |
|
P(x=1) |
= |
10 |
0.60000 |
0.00026 |
= |
0.0016 |
|
P(x=2) |
= |
45 |
0.36000 |
0.00066 |
= |
0.0106 |
|
P(x=3) |
= |
120 |
0.21600 |
0.00164 |
= |
0.0425 |
|
P(x=4) |
= |
210 |
0.12960 |
0.00410 |
= |
0.1115 |
|
P(x=5) |
= |
252 |
0.07776 |
0.01024 |
= |
0.2007 |
|
P(x=6) |
= |
210 |
0.04666 |
0.02560 |
= |
0.2508 |
|
|
|
|
|
|
|
|
|
|
|
|
P(x=0) + ,,, + P(x=6) = |
0.6177 |
||
|
|
P(x≥7) = 1 - P(x=0) - P(x=1) - … - P(x=6) = |
0.3823 |
||||
d) If n = 12 and p = 0.45, find P(5 ≤ x ≤ 7)
Tip: P(5 ≤ x ≤ 7) = P(X = 5) + P(X = 6) + P(X = 7)
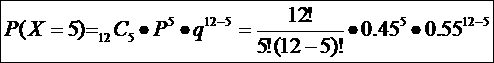
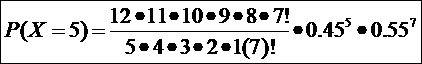
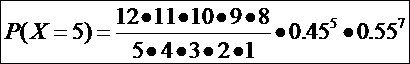
|
P(x=r) |
|
nCx |
px |
qn-x |
|
|
|
P(x=5) |
= |
792 |
0.018453 |
0.015224 |
= |
0.222498 |
|
P(x=6) |
= |
924 |
0.008304 |
0.027681 |
= |
0.212385 |
|
P(x=7) |
= |
792 |
0.003737 |
0.050328 |
= |
0.148945 |
|
|
|
|
P(5 ≤ x ≤ 7) |
= |
0.583828 |
|
